13. Volume
Recall: The Volume of a Solid computed using Thin Washers is \[ V=\int_a^b (\pi f(x)^2-\pi g(x)^2)\,dx \qquad \text{or} \qquad V=\int_a^b (\pi f(y)^2-\pi g(y)^2)\,dy \]
d1a. Volume using Thin Washers - Example
Find the volume of the solid of revolution obtained by revolving the region between the parabola \(y=x-\dfrac{x^2}{2}\) and the semicircle \(y=\sqrt{1-(x-1)^2}\) about the \(x\)-axis.
The graphs of the functions are shown in the figure. Since the curves are functions of \(x\), we do an \(x\) integral. So a Reimann sum rectangle is vertical. When we rotate about the \(x\)-axis, the rectangle sweepts out a washer.
From the figure, we see that the curves intersect at \(x=0\) and \(x=2\). However, we can also compute this by equating the functions as follows. We start by squaring both sides:
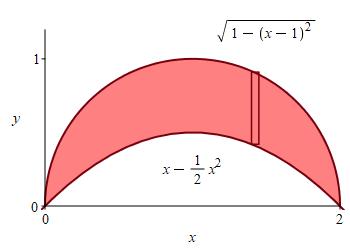
\[\begin{aligned} x-\dfrac{x^2}{2}&=\sqrt{1-(x-1)^2} \\ \left(x-\dfrac{x^2}{2}\right)^2&=1-(x-1)^2 \\ x^2-x^3+\dfrac{x^4}{4}&=-x^2+2x \end{aligned}\] We now take everything to one side of the equation, multiply through by \(4\) and factor the result: \[\begin{aligned} \dfrac{x^4}{4}-x^3+2x^2-2x&=0 \\ x^4-4x^3+8x^2-8x&=0 \\ x(x^3-4x^2+8x-8)&=0 \\ x(x-2)(x^2-2x+4)&=0 \end{aligned}\] So the limits are \(x=0\) and \(x=2\). Thus, the volume of the solid of revolution is given by: \[\begin{aligned} V&=\int_0^2 \pi(\text{upper})^2-\pi(\text{lower})^2\,dx \\ &=\pi\int_0^2 \left(\sqrt{1-(x-1)^2}\right)^2-\left(x-\dfrac{x^2}{2}\right)^2\,dx \\ &=\pi\int_0^2 \left(-x^2+2x-x^2+x^3-\dfrac{x^4}{4}\right)\,dx \\ &=\pi\left[ x^2-\dfrac{2x^3}{3}+\dfrac{x^4}{4}-\dfrac{x^5}{20}\right]_0^2 =\dfrac{16}{15}\pi \end{aligned}\]